Содержание
Курсовая работа «Расчет электрических фильтров» по дисциплине «Основы теории цепей»
Скачать МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант 01
Исходные данные
На входе полосового фильтра действуют периодические радиоимпульсы с параметрами:
период следования импульсов Tи = 105 мкс;
длительность импульсов tи = 40 мкс;
период несущей частоты Tн = 10 мкс;
амплитуда колебаний несущей частоты Um.н = 7 В.
Фильтр должен обеспечить максимально допустимое ослабление в полосе пропускания Аmax = ΔA = 3 дБ.
Полное ослабление на границах полос непропускания Апол = 23 дБ. Сопротивления нагрузок фильтра слева и справа Rг =Rн = 600 Ом.
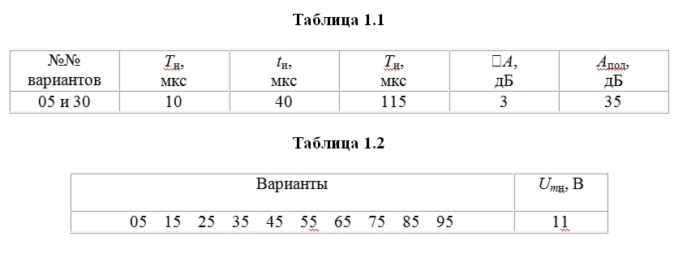
Вариант 05
Вариант 09
Требуется рассчитать двусторонне нагруженный пассивный полосовой LC-фильтр и активный полосовой RC-фильтр для выделения эффективной части спектра радиоимпульсов, лежащей в полосе частот от (fн – 1/tи) до (fн + 1/tи).
| №№ вариантов |
Тн, мкс |
tи, мкс |
Ти, мкс |
DА, дБ |
Апол, дБ |
| 09 и 34 | 10 | 40 | 150 | 3 | 21 |
|
Вариант |
Umн, В |
| 09 | 15 |
Вариант 12
На входе полосового фильтра действуют периодические радиоимпульсы (рисунок 1) с параметрами:
период следования импульсов Tи = 155 мкс ;
длительность импульсов tи = 40 мкс;
период несущей частоты Tн = 10 мкс;
амплитуда колебаний несущей частоты Um.н = 8 В.
Фильтр должен обеспечить максимально допустимое ослабление в полосе пропускания Аmax = ΔA = 1 дБ.
Полное ослабление на границах полос непропускания Апол = 24 дБ. Сопротивления нагрузок фильтра слева и справа Rг =Rн = 600 кОм. Характеристика фильтра аппроксимируется полиномом Чебышева.
Вариант 16
Таблица 1.1
| №№ вариантов |
Тн, мкс |
tи, мкс |
Ти, мкс |
DА, дБ |
Апол, дБ |
| 16 и 41 | 10 | 500 | 135 | 3 | 25 |
Таблица 1.2
| Варианты | Umн, В |
| 06 16 26 36 46 56 66 76 86 96 | 12 |
- РАСЧЁТ ПАССИВНОГО ПОЛОСОВОГО ФИЛЬТРА
1.1. Расчет амплитудного спектра радиоимпульсов
Находим несущую частоту
= 1/10*10-6 = 105 Гц
Рассчитываем частоты нулей огибающей спектра
= 105 +1/40*10-6 =1,25*105 Гц
= 106 +2/40*10-6 =1,5*105 Гц
= 106 -1/40*10-6 =0,75*105 Гц
106 -2/40*10-6 =0,5*105 Гц
Максимальное значение огибающей в виде напряжения, соответствующее частоте fн, находится по формуле:
= 7В*40*10-6 /(2*105*10-6 ) = 1,33 В
Зная максимальное значение и расположение нулей по оси частот, можно построить огибающую дискретного спектра периодических радиоимпульсов. Но предварительно рассчитаем спектральные составляющие с частотами , располагающиеся симметрично относительно несущей частоты.


1. Задание на курсовую работу
Задание на курсовую работу составлено по стовариантной системе. Номер варианта определяется двумя последними цифрами в номере зачет-ной книжки студента.
На входе полосового фильтра действуют периодические прямо-угольные радиоимпульсы (рис. 1.1) с параметрами: tи – длительность им-пульсов, Tи – период следования; Tн – период несущей частоты; Umн – ам-плитуда несущего колебания, имеющего форму гармонического uн(t) = = Umн cos нt.
Требуется рассчитать двусторонне нагруженный пассивный поло-совой LC-фильтр и активный полосовой RC-фильтр для выделения эф¬фективной части спектра радиоимпульсов, лежащей в полосе частот от (fн – 1/tи) до (fн + 1/tи) (главный «лепесток спектра»). График модуля спек-тральной функции U(f) = |U(jf)| радиоимпульса приведен на рис. 1.2. Спектр имеет дискретный характер, поэтому частоты fп1 и fп2 границы по-лосы пропускания фильтров определяются крайними частотами в главном «лепестке спектра». Частоты fз1 и fз2 полосы задерживания (непропуска-ния) фильтра определяются частотами первых дискретных составляющих, лежащими слева от (fн – 1/tи) и справа от (fн + 1/tи). Конкретное определе-ние численных значений всех частот показано в типовом примере расчета LC-фильтра.
Исходные данные для расчета приведены в таблицах 1.1 и 1.2. Сопро-тивления генератора радиоимпульсов Rг и сопротивление нагрузки Rн пас-сивного фильтра одинаковы: Rг = Rн = R. Для вариантов 0125 и 5175 R = 600 Ом, для вариантов 2650 и 7699 R = 1000 Ом. Характеристика фильтра аппроксимируется полиномом Чебышева.
Таблица 1.2
Варианты Umн, В
00 10 20 30 40 50 60 70 80 90
01 11 21 31 41 51 61 71 81 91
02 12 22 32 42 52 62 72 82 92
03 13 23 33 43 53 63 73 83 93
04 14 24 34 44 54 64 74 84 94
05 15 25 35 45 55 65 75 85 95
06 16 26 36 46 56 66 76 86 96
07 17 27 37 47 57 67 77 87 97
08 18 28 38 48 58 68 78 88 98
09 19 29 39 49 59 69 79 89 99 6
7
8
9
10
11
12
13
14
15
В ходе выполнения курсовой работы необходимо:
1. Рассчитать и построить график амплитудного спектра радиоимпульсов.
2. Определить частоты fп2 и fз2 и рассчитать превышение амплитуды час-тоты fп2 над амплитудой частоты fз2 в децибелах в виде соотношения А = 20lgUmп/Umз на входе фильтра.
3. Рассчитать минимально допустимое ослабление фильтра в полосе за-держивания Аmin = Апол – А.
4. Рассчитать порядок m НЧ-прототипа требуемого фильтра.
5. Получить выражение для передаточной функции НЧ-прототипа при ап-проксимации его характеристики полиномом Чебышева.
6. Осуществить реализацию двухсторонне нагруженного полосового LC-фильтра.
7. Осуществить реализацию полосового ARC-фильтра.
8. Привести ожидаемую характеристику ослабления полосового фильтра в зависимости от частоты, т. е. A = K(f).
9. Рассчитать ослабление ARC-фильтра на границах полосы пропускания и полосы непропускания (задерживания).
10. Привести схему ARC-полосового фильтра.
2. Основные сведения из теории фильтрующих цепей
Электрические фильтры – это линейные четырехполюсники, обла-дающие избирательными свойствами: они предназначены для выделения из состава сложного электрического колебания частотных составляющих определенного спектра частот, лежащего в полосе пропускания (ПП), и подавления тех составляющих, частоты которых лежат за пределами ПП, т. е. в полосе непропускания (ПН) или полосе задерживания (ПЗ). Между этими полосами находится переходная область. На рис. 2.1 приведены структурные характеристики ослабления фильтра нижних частот (ФНЧ) и полосового фильтра (ПФ). Для ФНЧ полоса пропускания лежит в диапазо-не частот 0 fп, а непропускания – в диапазоне fз (рис. 2.1, а); для ПФ полоса пропускания fп1 fп2 располагается между полосами непропускания 0 fз1 и fз2 (рис. 2.1, б).
Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик. Так ослабление в ПП не должно превышать максимально допустимого ослабления Аmax = А, а в ПН не должно быть ниже значения Аmin. Требования к дру-гим характеристикам фильтров здесь не рассматриваются. Схема подклю-чения фильтра к источнику сигнала приведена на рис. 2.2.
Синтез (расчет) фильтров состоит из двух этапов: этапа аппроксима-ции и этапа реализации. На первом этапе по заданным Аmin и Аmax в ПП и ПН формируется передаточная функция фильтра, т. е. математическое описание цепи, которая удовлетворяет указанным выше требованиям. На втором этапе создают схему цепи и определяют значения ее элементов по полученной передаточной функции.
Оба этапа хорошо разработаны применительно к синтезу ФНЧ. Что касается синтеза других типов фильтров: полосовых, заграждающих (ре-жекторных), фильтров верхних частот, – то возможны различные вариан-ты расчета. Один из них основан на том, что требования к заданному фильтру пересчитываются в требования к его НЧ-прототипу на основании принципа преобразования частоты. Рассчитывается НЧ-прототип по мето-дике синтеза ФНЧ. Затем полученная схема НЧ-прототипа преобразуется в схему заданного фильтра, но только в случае пассивных фильтров [13]. В случае активных фильтров этап реализации осуществляется другим мето-дом.
2.1. Синтез пассивных полосовых фильтров
Этап аппроксимации. Задано: частоты fп1 и fп2 – границы ПП и час-тота fз2 – граница ПН справа; ослабление Аmin и Аmax = А (рис. 2.1, б). Ис-пользуя понятие центральной частоты или средней геометрической часто-ты ПП и ПН
(2.1)
находим значение fз1 – граничной частоты ПН слева.
Требования к характеристикам ПФ пересчитываются в требования к его НЧ-прототипу:
(2.2)
при тех же значениях Аmin и Аmax (рис. 2.1, а).
Зная требования к ослаблению ФНЧ можно пересчитать их в требова-ния к АЧХ ФНЧ или, как это принято в теории фильтров, в требования к квадрату АЧХ |H(j2f)|2 = |H(j)|2. Для унификации расчетов вместо уг-ловой частоты вводят понятие нормированной частоты = /н, где н – нормирующая частота. Обычно в качестве н выбирают граничную частоту ПП ФНЧ. Тогда
(2.3)
При синтезе ФНЧ используются универсальные соотношения [1]:
(2.4)
(2.5)
где () – функция фильтрации; – коэффициент неравномерности ос-лабления в ПП. Если в качестве () используются полиномы, то фильт-ры называются полиномиальными. Среди последних наиболее широкое применение нашли фильтры Баттерворта и Чебышева.
У фильтров Баттерворта () = Вm() = m, где m – порядок фильт-ра. Характеристика H2() = |H(j)|2, т. е. квадрата коэффициента переда-чи для таких фильтров разного порядка m приведена на рис. 2.3, а (кривая 1 – характеристика идеального ФНЧ, кривая 2 для m = 6, кривая 3 для m = 2). При = 1 все кривые проходят через точку, зависящую от . Из анализа рисунка видно, что действительно определяет неравномерность коэффициента передачи ФНЧ в ПП.
Если в (2.4) положить () = Вm(), а j = р, то после преобразова-ний получим передаточную функцию фильтра в виде
(2.6)
где H0 = 1/.
У фильтров Чебышева функция фильтрации () = Тm() = = cosm arccos для области нормированных частот –1 1. Харак-теристика квадрата коэффициента передачи при разных m показана на рис. 2.3, б (кривая 1 – характеристика идеального ФНЧ, кривая 2 для m = 4, кривая 3 для m = 2). Анализ кривых на рис. 2.3, б показывает, что полином Чебышева в интервале 0 1 принимает экстремальные значения (min или max) m + 1 раз. Или по иному: порядок фильтра нижних частот Чебышева по кривой H2(), или по любой другой частотной характери-стике фильтра, определяется удвоенным количеством периодов колебаний в ПП, рассчитанном на уровне полосы пропускания. На рис. 2.3, б: граница полосы пропускания по частоте – это = 1; уровень полосы пропускания – это 1/(1 + 2).
Передаточная функция фильтра Чебышева описывается тем же выра-жением (2.6), но коэффициент H0 = 1/(2m–1).
Анализ кривых на рис. 2.3 показывает, что:
– чем выше порядок фильтра, тем выше его избирательность за счет уменьшения переходной области;
– при одинаковом порядке m избирательность фильтров Чебышева выше избирательности фильтров Баттерворта;
– у фильтров Чебышева ФЧХ в полосе пропускания имеет нелинейный характер за счет волнового характера изменения Н2() в ПП.
Итак, этап аппроксимации при синтезе ПФ заканчивается получением функции H(p) для НЧ-прототипа.
Этап реализации. Если фильтр со стороны зажимов 1–1 рассматри-вать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой Rн (рис. 2.2), то, можно оперировать понятием входного сопро-тивления Zвх.1(р) двухполюсника со стороны зажимов 1–1:
(2.7)
где (р) – коэффициент отражения, характеризующий несогласованность между сопротивлениями Rг и Zвх.1(р). Если известно Zвх.1(р), то двухпо-люсник можно реализовать, например, методом Дарлингтона [1, 2]. Один из возможных вариантов реализации схемы названным методом сводится к следующему. Осуществляют нормирование Zвх.1 по сопротивлению, вы-бирая в качестве нормирующего, сопротивление Rг, а коэффициент отра-жения записывают через табулированный полином h(р): (р) = h(р)/v(р). Тогда (2.7) записывают как
(2.8)
Например, для фильтров Чебышева третьего порядка сам полином Чебышева равен:
(2.9)
а полином h(р) будет:
(2.10)
Подставляя h(р) из (2.10) и v(р) из (2.6) в (2.8), записывают Zвх.1(р) в виде цепной дроби и по ней составляют схему двухполюсника, т. е. LC-фильтра нижних частот, нагруженного на сопротивление Rн. Элементы этой схемы представлены величинами, нормированными по частоте и по сопротивлению. Поэтому следующей операцией расчета является опера-ция денормирования значения элементов НЧ-прототипа. После этого, ис-пользуя формулы преобразования частоты, переходят от схемы НЧ-прототипа к схеме полосового фильтра. Элементы схемы ПФ, очевидно, будут иметь сразу реальные значения.
2.2. Синтез активных полосовых фильтров
ARC-фильтры представляют собой комбинацию пассивной RC-цепи и активного элемента. В качестве последнего чаще всего используются опе-рационные усилители часто с двумя входами – инвертирующим и неин-вертирующим. В схемах ARC-фильтров обязательно имеется обратная связь. Известно [1, 2], что передаточная функция любой активной цепи с обратной связью записывается как
где Нус(р) и Нос(р) передаточные функции цепи прямого усиления и цепи обратной связи соответственно. Знаменатель Н(р) – это полином, напри-мер, второй степени. Корни его, т. е. полюсы Н(р) могут быть в том числе и комплексно-сопряженными. Последнее означает, что ARC-цепь эквива-лентна пассивной LC-цепи, а т. к. LC-цепь обладает избирательными свой-ствами, то и ARC-цепь тоже может обладать избирательными свойствами, т. е. является фильтром.
Синтез ARC-фильтров, как и пассивных LC-фильтров, состоит из двух этапов: этапа аппроксимации и этапа реализации. Этап аппроксимации в обоих случаях одинаков. Этап реализации для ARC-фильтров – отличает-ся от LC-реализации.
Этап реализации. Вначале осуществляют переход от передаточной функции НЧ-прототипа, которая имеет вид (2.6), к передаточной функции полосового фильтра. Один из возможных вариантов такого перехода осно-ван на использовании формулы пересчета полюсов НЧ-прототипа в полю-сы ПФ:
(2.11)
где
– полюсы передаточной функции НЧ-прототипа;
0 = 2f0 – находится по (2.1).
Согласно (2.11) одной паре комплексно-сопряженных полюсов нор-мированной передаточной функции НЧ-прототипа соответствует две пары комплексно-сопряженных полюсов денормированной передаточной функ-ции полосового фильтра. Одному вещественному полюсу (рнч.нор = + j0) нормированной H(р) НЧ-прототипа (2.6) соответствует одна пара ком-плексно-сопряженных полюсов вида денормированной H(р) полосового фильтра. В результате общий порядок ПФ удваивается по сравнению с порядком НЧ-прототипа.
Передаточную функцию ПФ удобно представлять произведением сомно-жителей второго порядка H1(р), H2(р), H3(р) и т. д. Каждый из этих сомно-жителей реализуется в виде активного RC-звена второго порядка, а получен-ные звенья соединяются каскадно, образуя полную схему ПФ. Звенья ARC-фильтров в общем случае являются типовыми (одинаковыми) для фильтров, имеющих одинаковое расположение полосы пропускания на шкале частот.
3. Пример расчета полосового LC-фильтра
Согласно заданию на курсовую работу на входе полосового фильтра действуют периодические радиоимпульсы (рис. 1.1) с параметрами: пе-риод следования импульсов Tи = 800 мкс; длительность импульсов tи = 200 мкс; период несущей частоты Tн = 33,3 мкс; амплитуда колебаний несущей частоты Um.н = 5 В. Фильтр должен обеспечить максимально до-пустимое ослабление в полосе пропускания Аmax = A = 3 дБ. Полное ос-лабление на границах полос непропускания Апол = 24,2 дБ. Сопротивления нагрузок фильтра слева и справа Rг = Rн = 1 кОм (рис. 2.2). Характеристи-ка фильтра аппроксимируется полиномом Чебышева.
3.1. Расчет амплитудного спектра
радиоимпульсов
Прежде чем приступать непосредственно к расчету фильтра, необхо-димо определить частотный состав сигнала, поступающего на вход фильт-ра, т. е. рассчитать и построить график амплитудного спектра периодиче-ских радиоимпульсов, взяв за основу рис. 1.2.
Вначале находится несущая частота:
Затем рассчитывают частоты нулей огибающей спектра. Они зависят от длительности импульса:
Максимальное значение огибающей в виде напряжения, соответст-вующее частоте fн, находится по формуле
(3.1)
Зная максимальное значение и расположение нулей по оси частот, строим огибающую дискретного спектра периодических радиоимпульсов в виде пунктирной кривой в масштабе по оси частот (рис. 1.2).
Внутри огибающей находятся спектральные составляющие или гар-моники спектра с частотами fi, где i – номер гармоники. Они располагают-ся симметрично относительно несущей частоты, зависят от периода следо-вания импульсов и находятся по формуле
.
Учитывая, что
рассчитываем частоты гармоник, лежащих только справа от fн:
Частоты гармоник, лежащих слева от fн, будут:
Амплитуды напряжения i-ых гармоник находятся по формуле
(3.2)
где K = tи/Tн – количество периодов несущих колебаний косинусоидаль-ной формы в импульсе. Например, на рис. 1.1 К = 4, а в рассматриваемом примере К = 6.
Из анализа рис. 1.2 видно, что главный «лепесток спектра» занимает диапазон частот от 25 до 35 кГц. Крайние частоты диапазона совпадают с нулями огибающей, поэтому их амплитуды равны нулю, в частности Um.4 = 0, Um.(–4) = 0.
После расчета амплитуд по (3.2) их значения отражаются в виде дис-кретных составляющих внутри огибающей спектра (рис. 1.2).
Полезно обратить внимание на характерную особенность спектра, связанную с понятием скважности импульсов. Если скважность q, т.е. от-ношение периода следования импульсов Tи к длительности импульсов tи, равна целому числу, то в спектре отсутствуют гармоники с номерами, кратными скважности. В рассматриваемом примере q = 4, поэтому в спек-тре будут отсутствовать (совпадать с нулями огибающей) 4, 8, 12 и т.д. гармоники слева и справа от несущей частоты.
3.2. Формирование требований к полосовому фильтру
Учитывая, что амплитуды спектральных составляющих на частотах 25 и 35 кГц равны нулю, примем за эффективную часть спектра, которую нужно выделить полосовым фильтром, диапазон частот от 26,25 кГц до 33,75 кГц. Следовательно, эти частоты будут определять частоты границы полосы пропускания фильтра fп1 и fп2 соответственно (рис. 2.1, б). Гранич-ную частоту полосы непропускания fз2 выбираем равной частоте первой гармоники спектра сигнала, находящейся после частоты (fн + 1/tи) = 35 кГц. Этой частотой является частота f5 = 36,25 кГц. Следовательно, fз2 = = f5 = 36,25 кГц.
Используя (2.1), найдем центральную частоту ПП:
Тогда граничная частота fз.1 полосы непропускания будет
Минимально-допустимое ослабление фильтра в ПН зависит от разницы амплитуд гармоник f3 и f5 спектра сигнала на выходе фильт-ра, выраженной в децибелах и заданной величиной Апол – полного ос-лабления:
(3.3)
где
(3.4)
исходная разница амплитуд третьей и пятой гармоник в децибелах, най-денная в ходе расчета спектра радиоимпульсов.
Согласно (3.2):
По (3.4) находим
а из (3.3)
Таким образом, требования к полосовому фильтру сводятся к сле-дующему:
Аппроксимация передаточной функции должна быть выполнена с по-мощью полинома Чебышева.
3.3. Формирование передаточной функции
НЧ-прототипа
Используя (2.2), находим граничные частоты ПП и ПН НЧ-прототипа.
По формулам (2.3) получаем значения нормированных частот
Требования к НЧ-прототипу могут быть проиллюстрированы рисун-ком 3.1.
Находим коэффициент неравномерности ослабления фильтра в ПП из рассмотрения (2.5) при A = A и = 1, когда (1) = Тm(1) = 1:
Порядок фильтра Чебышева находится также из рассмотрения (2.5), но при A = Amin и =з, т. е. ослабление рассматривается в полосе непро-пускания. А в ПН полином Чебышева Тm() = chmarch, поэтому
(3.5)
Для вычисления функции archх рекомендуется соотношение
После подстановки в (3.5) исходных данных и вычислений получим m = 2,9. Расчетное значение m необходимо округлить в бóльшую сторону до целого числа. В данном примере принимает m = 3.
Примечание. При достаточно точных расчетах значение m во всех ва-риантах задания должно лежать в пределах 2 < m < 3. Если так не получи-лось необходимо обратиться за консультацией на кафедру.
Пользуясь таблицей 3.1, находим полюсы нормированной передаточ-ной функции НЧ-прототипа:
(3.6)
Обратить внимание на то, что полюсы расположены в левой полу-плоскости комплексной переменной р.
Формируем нормированную передаточную функцию НЧ-прототипа в виде
где v(р) – полином Гурвица, который можно записать через полюсы:
Производя вычисления, получим
(3.7)
Обратить внимание на то, что в (3.7) числитель равен свободному члену полинома знаменателя.
При расчетах необходимо придерживаться точности не менее шести значащих цифр после запятой.
3.4. Реализация LC-прототипа
Для получения схемы НЧ-прототипа воспользуемся методом Дар-лингтона, когда для двусторонне нагруженного фильтра (рис. 2.2) состав-ляется выражение для входного сопротивления Zвх.1(р) (2.8). Подставляя в (2.8) значение v(р) из (3.7) и значение h(p) из (2.10), после преобразований получим
(3.8)
Формула (3.8) описывает входное сопротивление двухполюсника (со-гласно схеме на рис. 2.2 фильтр, нагруженный на сопротивление Rн, это действительно двухполюсник). А если известно выражение для входно-го сопротивления, то можно построить схему двухполюсника, восполь-зовавшись, например, методом Кауэра [16]. По этому методу формула для Zвх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, (3.8) преобра-зуется к виду
(3.9)
после чего производится ряд последовательных делений. Вначале числи-тель делим на знаменатель:
Затем первый делитель делим на первый остаток:
Второй делитель делим на второй остаток:
Третий делитель делим на третий остаток:
Получили четыре результата деления, которые отражают четыре нор-мированных по частоте и по сопротивлению элемента схемы в виде значе-ний их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деле-ния следует, что он отражает емкостную проводимость, поэтому все вы-ражение (3.9) можно записать в виде цепной дроби:
(3.10)
По формуле (3.10) составляем схему (рис. 3.2), на которой С1н = 3,349; L2н = 0,712; С3н = 3,349; Rг.н = Rн.н = Rнор.
Денормируем элементы схемы НЧ-прототипа, используя соотноше-ния:
(3.11)
где н = п.нч – нормирующая частота;
Rг – нормирующее сопротивление, равное внутреннему сопротивле-нию источника сигнала.
Используя соотношения (3.11) и значения н и Rг получаем реальные значения элементов схемы НЧ-прототипа:
3.5. Реализация пассивного полосового фильтра
Из теории фильтров известно [16], что между частотами НЧ-прототипа и частотами пф полосового фильтра существует соотношение
(3.12)
где 0 находится по (2.1).
На основании (3.12) индуктивное сопротивление НЧ-прототипа заме-няется сопротивлением последовательного контура с элементами
(3.13)
а емкостное сопротивление НЧ-прототипа заменяется сопротивлением па-раллельного контура с элементами
(3.14)
Тогда, на основании схемы ФНЧ, изображенной на рис. 3.2 может быть построена схема полосового фильтра так, как это показано на рис. 3.3. Элементы этой схемы рассчитываются по формулам (3.13) и (3.14).
На этом расчет полосового LC-фильтра заканчивается.
4. Пример расчета активного полосового фильтра
4.1. Расчет полюсов ARC-фильтра
Требования к полосовому ARC-фильтру остаются теми же, что и к полосовому LC-фильтру. Поэтому на этапе аппроксимации синтеза ARC-фильтра можно воспользоваться результатами расчета LC-фильтра, полученными в разделах 3.13.3. Причем, не самой нормированной пе-редаточной функцией (3.7), а только ее полюсами (3.6), и, согласно (2.11), найти полюсы денормированной передаточной функции ПФ. Вначале находим:
Затем сами полюсы:
(4.1.а)
(4.1) (4.1.б)
(4.1.в)
Расчет показывает, что вместо трех полюсов нормированной переда-точной функции НЧ-прототипа получается шесть полюсов передаточной функции ARC полосового фильтра, причем денормированной. Их значения удобно представить в виде таблицы 4.1.
Таблица 4.1
Номера
полюсов Полюсы H(p)
1,2 0,7032 18,676
3,6 0,3844 20,9351
4,5 0,3188 16,6781
Следует отметить, что чередование пар полюсов в таблице 4.1 значе-ния не имеет.
4.2. Формирование передаточной функции
Учитывая, что ARC-фильтры обычно строятся из каскадно-соеди¬ненных звеньев второго порядка, целесообразно передаточную функцию таких фильтров формировать из произведения сомножителей тоже второго порядка. Они имеют вид [1, 2]:
Тогда вся передаточная функция рассчитываемого фильтра будет:
(4.2)
Коэффициенты в числителе могут иметь одинаковую величину и рас-считываться по формуле
Коэффициенты в знаменателе (4.2) находятся по формулам:
(4.3)
где – значение полюсов (4.1). Например,
14064;
Значения всех рассчитанных коэффициентов сведены в таблицу 4.2.
Таблица 4.2
Номер
сомножителя Значения коэффициентов
ai1 bi1 bi0
1
2
3 2,9624104
2,9624104
2,9624104 1,4064104
0,7688104
0,6376104 3,49291010
4,384261010
2,78261010
Подставляя найденные коэффициенты в 4.2 получим:
(4.4)
4.3. Расчет элементов схемы фильтра
В качестве типовой выбираем простейшую схему ПФ на одном опе-рационном усилителе (ОУ) (рис. 4.1). Если составить эквивалентную схе-му, заменив ОУ ИНУНом, то, используя любой из методов анализа цепей [1], можно получить передаточную функцию, описывающую работу схе-мы на рис. 4.1, в виде
(4.5)
Из (4.5) видно, что рассмотренная схема является схемой второго по-рядка. Следовательно, для реализации функции (4.4) потребуется три по-добных схемы или три звена, соединенных каскадно. Расчет элементов этих схем R1; R2; С3; С4; R5 ведется путем сравнения идентичных коэффи-циентов в формулах (4.4) и (4.5).
Для первого звена ПФ берутся коэффициенты из первого сомножите-ля (4.4):
(4.6)
В системе (4.6) пять неизвестных и только три уравнения. Система нерешаема. Поэтому рекомендуется задаваться значениями, например, ем-костей конденсаторов С3 и С4 (в ходе настройки фильтра при его изготов-лении принято использовать переменные сопротивления, т. к. переменных конденсаторов с большой емкостью нет вообще).
Если принять С3 = С4 = 2 нФ, то решая (4.6), получим:
R1 = 17 кОм, R5 = 71 кОм, R2 = 101 Ом.
Составляя аналогичную систему для второго звена при тех же С3 = = С4 = 2 нФ, получим:
R1 = 17 кОм, R5 = 130 кОм, R2 = 44 Ом.
Аналогично для третьего звена:
R1 = 17 кОм, R5 = 157 кОм, R2 = 58 Ом.
Рассчитанные сопротивления не соответствуют стандартным номина-лам резисторов. Поэтому для сопротивлений R1 и R5 в каждом звене бе-рутся резисторы с номиналом, ближайшим к рассчитанному значению. Сопротивление R2 берется составным, из последовательно соединенных постоянном и переменном резисторов, что позволит осуществлять общую настройку фильтра.
5. Проверка результатов расчета
Проверка расчетов может быть выполнена в двух вариантах. Первый вариант – проверяется только этап аппроксимации, когда определяется на-сколько точно созданная передаточная функция соответствует исходным требованиям к фильтру по ослаблению в ПП и в ПН. Второй вариант – проверяется точность уже всего расчета, когда по известной передаточной функции схемы фильтра (т. е. с учетом значений элементов схемы) рас-считывается и строится график H(f) или А(f) всей схемы фильтра и анали-зируется, насколько хорошо этот график соответствует исходных требова-ниям по ослаблению в ПП и в ПН. Конечно, второй вариант для разработ-чика предпочтительнее.
При синтезе пассивного полосового фильтра получена передаточная функция только НЧ-прототипа (3.7) и в этом случае возможен только пер-вый вариант проверки. При синтезе активного ПФ известна передаточная функция одного звена уже самой схемы фильтра (4.5). Очевидно, что Н(р) всего фильтра будет
(5.1)
где значения каждого сомножителя будут отличаться из-за разницы в зна-чениях сопротивлений звеньев фильтра. Итак, формула (5.1) позволяет реализовать второй вариант проверки выполненных расчетов.
С этой целью в (4.5) производится замена переменной вида р = j, в результате чего получают выражение
Находится модуль H(j) в виде
(5.2)
Зная H(), легко найти зависимость ослабления от частоты вначале каждого звена, а затем всего фильтра:
(5.3)
где
(5.4)
В качестве числового примера выполним расчет первого звена фильтра.
Из раздела 4.3 берем значения элементов:
С1 = С2 = 2 нФ, R1 = 17 кОм, R2 = 101 Ом, R5 = 71 кОм.
Подставляем эти значения в (5.2)
На частоте границы ПП fп2 = 33,75 кГц находим Н1(п2) = 0,6. На час-тоте границы ПН fз2 = 36,25 кГц находим Н1(з2) = 0,387. Кроме того на-ходим Н1() на частотах. fп1 = 26,25 кГц и fз1 = 24,43 кГц.
Аналогичные расчеты выполняем для второго и третьего звеньев. Ос-лабления рассчитываются по формулам (5.3) и (5.4). Все результаты сво-дятся в таблицу 5.1.
При анализе табличных данных обратить внимание на разный харак-тер зависимости ослабления от частоты у разных звеньев фильтра. Если сравнивать рассчитанное ослабление всей схемы фильтра на частотах границ ПП и ПН с заданным ослаблением на этих же частотах (раз-дел 3.2), то можно сделать вывод о довольно хорошем их соответствии. При практическом изготовлении фильтров всегда предусматривается операция по их настройке, в ходе которой добиваются ослабления с тре-буемой точностью.
В ходе расчета по формуле (5.2) обратить внимание на то, что значение Н() наиболее сильно зависит от величины сопротивления R2, поэтому именно это сопротивление необходимо выбирать пере-менным.
На рис. 5.1 приведена ожидаемая теоретическая кривая зависимости ослабления фильтра от частоты. На рис. 5.2 приведена принципиальная схема активного полосового фильтра.
6. Вопросы для подготовки к защите
курсовой работы
1. Дайте определение электрического фильтра.
2. Как классифицируются фильтры по диапазону пропускаемых ими час-тот.
3. В чем заключаются требования к электрическим характеристикам фильтров.
4. Что такое функция фильтрации.
5. Что значит осуществить нормирование по частоте; по сопротивлению. В чем сущность денормирования.
6. Фильтры Баттерворта. Начертить графики зависимости ослабления и квадрата модуля передаточной функции от нормированной частоты для ФНЧ.
7. Тоже самое для фильтров Чебышева.
8. В чем достоинства и недостатки фильтров Баттерворта и Чебышева.
9. Как пересчитать требования к характеристикам ПФ, ФВЧ в требования к НЧ-прототипу.
10. Порядок синтеза пассивных полосовых фильтров.
11. Порядок синтеза активных полосовых фильтров.
12. Начертите графики ослабления ПФ для фильтров Баттерворта и Че-бышева для разных порядков фильтров.
13. Как изменяется амплитудный спектр периодических радиоимпульсов при изменении их длительности периода следования и периода несу-щей частоты.