Вычислительная математика

Вариант 14

ЗАДАНИЕ 1.

Решить методом Гаусса систему линейных уравнении.

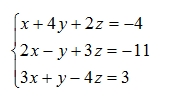
ЗАДАНИЕ 2 Дано нелинейное алгебраическое уравнение

х4 -8х2 +2х2 — 3 = 0.

2.1 Найти значение этого выражения на концах заданного отрезка и оценить наличие корней. Методом бисекции, с точностью 0,01 найти корень уравнения, локализованный на отрезке [1, 4].

2.2 Методом Ньютона с точностью 0,001 найти корень уравнения, локализованный на отрезке [1, 4]. В качестве исходного приближения сначала выбрать конец исходного отрезка, затем начало и после — среднюю точку. По результатам расчета сделать выводы

ЗАДАНИЕ 3

Решить систему нелинейных уравнений методом Ньютона с точностью 0,001.

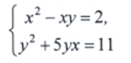
ЗАДАНИЕ 4

Записать формулы правой, левой, центральной разностной производной и четырех точечную формулу дифференцирования для численного дифференцирования функции

Используя эти формулы найти производную функции в точке х = 1 с шагом h = 0,5, сделать вывод и оценить погрешность вычисления.

ЗАДАНИЕ 5.

Записать формулы трапеций и Симпсона для вычисления интеграла

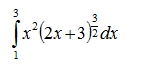
Вычислить интеграл по этим формулам, разбивая отрезок интегрирования на n = 10 частей, определить погрешность вычисления, сделать вывод.