Лабораторная работа №3 Исследование согласованного фильтра дискретных сигналов известной формы

По дисциплине: «Общая теория связи»

В вариантах 01 и 02 читаем пояснения красным на 3ей странице

РАБОТА № 1 Исследование помехоустойчивости дискретных видов

РАБОТА № 2 Исследование помехоустойчивости методов передачи и приема дискретных сигналов на автоматизированном рабочем месте СПИ

РАБОТА № 3 Исследование согласованного фильтра дискретных сигналов известной формы

РАБОТА № 4 (14) Исследование обнаруживающей и исправляющей способности циклических кодов

РАБОТА № 5 (15) Исследование эффективности устройств защиты от ошибок в дискретном канале передачи информации

Вариант 01

Вариант 02

Вариант 03

Вариант 04

Вариант 05

Сделано под день рождения

Вариант 08

Цель работы:

Экспериментальное исследование характеристик сложных дискретных сигналов и особенностей их приёма согласованным фильтром.

Описание лабораторной установки:

Лабораторная установка выполнена в виде программно управляемой модели на ПЭВМ в составе штатного оборудования (процессор, дисковод, дисплей, принтер).

Краткое описание структурной схемы исследуемого оптимального (согласованного) фильтра, изображенного на рисунке 1, приводится ниже.

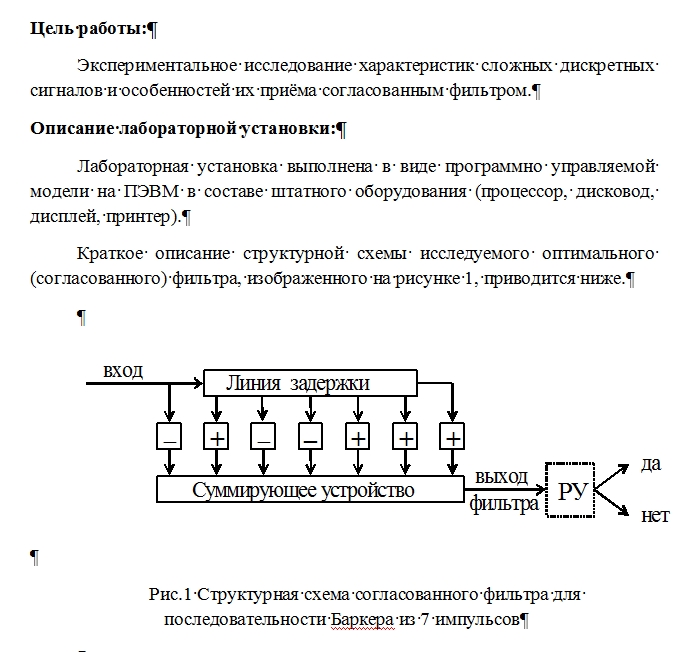
Рис.1 Структурная схема согласованного фильтра для последовательности Баркера из 7 импульсов

Импульсы последовательности Баркера (n=7), длительностью T=n×tи
поступают на линию задержки, имеющую отводы через каждые tи , и далее через инвертирующие или не инвертирующие устройства (в соответствии с формой последовательности) на сумматор. Сигнал на выходе суммирующего
устройства после 2×n тактовых интервалов tи имеет вид функции корреляции входной последовательности. Для обнаружения сигнала на выходе фильтра может устанавливаться решающее устройство (РУ), в котором сигнал на выходе сумматора сравнивается с пороговым уровнем и принимается решение о присутствии на входе фильтра (да) или отсутствии (нет) данной последовательности Баркера.

Лабораторное задание:

1. Ознакомиться с особенностями экспериментального исследования на ЭВМ приёма дискретных сигналов согласованным фильтром (СФ).
2. Исследовать связь между импульсной характеристикой СФ и видом сигнала, с которым он должен быть согласован.
3. Исследовать форму сигнала на выходе согласованного фильтра при подаче на его вход различных сигналов (согласованного и несогласованного с фильтром, в том числе и инвертированного).

Ход работы:

1. Исследовать связь между импульсной характеристикой согласованного фильтра и видом сигнала, с которым он должен быть согласован.

В качестве исходного сигнала используем дискретные кодовые последовательности из элементов {+1,- 1}  длиной n,

Но для варианта 01 дана комбинация из 3-х символов, а программа начинает работать минимум с 5-ю. Поэтому выбираем подходящую из существующих вариантов.

{+1,+1,+1,-1,-1,+1,-1}

Данный сигнал используется для последующих предварительных расчётов и выполнения лабораторной работы в соответствии с методическими указаниями к ней.

Для выбранной последовательности S(t) найдём требуемую импульсную характеристику g(t) фильтра, который должен быть согласован с S(t). Функция g(t) является зеркальным отображением сигнала S(t), т.е.

g(t)=-1,1,-1,-1,1,1,1.

Запустим на ЭВМ программу ДО SFiltr.exe, введём с клавиатуры длину последовательности n=7, временную функцию сигнала S(t) и импульсную характеристику фильтра g(t).

Получим графики S(t) и g(t):

Из графиков видно, что импульсная характеристика является зеркальным отображением сигнала S(t).

2. Исследовать форму сигнала на выходе согласованного фильтра при вводе сигнала, с которым он согласован.

Для этого предварительно рассчитаем временную функцию ожидаемого сигнала на выходе фильтра y(t) в виде последовательности значений для дискретных моментов времени tk = k×tи, где –n £ k £ n. Pасчёт у(k×tи) основан на том, что напряжение на выходе СФ представляет собой по форме корреляционную функцию входного сигнала. Для корреляционной функции дискретного сигнала общего вида применима формула

,

здесь n указывает количество элементов, на которое осуществляется сдвиг (n – целое число, положительное, отрицательное или нуль), так как важнейшей операцией при корреляционной обработке дискретных сигналов с использованием согласованного фильтра является поэлементный сдвиг такого сигнала. При n>0 сигнал сдвигается вправо, а при n<0 сигнал сигнал сдвигается влево. По выше указанной формуле получим:

Введём полученные значения с клавиатуры по запросу ЭВМ в следующем порядке: 0,-1,0,-1,0,-1,0,7,0,-1,0,-1,0,-1,0.

На выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, которая имеет значительный максимум (пик).

4. Исследовать форму сигнала на выходе согласованного фильтра при вводе различных сигналов, с которыми фильтр не согласован, в том числе и сигнала, инвертированного по отношению к S(t).

Изменим в последовательности S(t) 1 элемент:

При вводе сигнала, с которым фильтр не согласован (отличается от используемой последовательности S(t) одним элементом), на выходе получаем сигнал с меньшим максимумом и разным уровнем боковых выбросов (уровень бокового выброса увеличился).

Изменим в последовательности S(t) 2 элемента:

Получим сигнал с ещё меньшим пиком.

Изменим в последовательности S(t) 3 элемента:

Изменились  уровни боковых выбросов.

При подаче на вход СФ несогласованного сигнала, сигнал на выходе несимметричен (искажен).

Введём сигнал, инвертированный по отношению к S(t):

Форма сигнала на выходе СФ, при подаче инвертированного сигнала зеркально отражен от первого.

Вывод:

Сложные сигналы должны …..